Dot Product of Two Vectors
This angle decides whether the dot product will be positive or negative or bigger or smaller in value. For the dot product of two vectors the two vectors are expressed in terms of unit vectors i j k along the x y z axes then the scalar product is obtained as follows.
The angle between the two vectors is significant.

. Then the dot product is calculated as. Dot Product of Two Sparse Vectors. That description probably doesnt help much.
Angle between vectors in three dimensions. Determine if the following vectors are orthogonal. We can simply multiply the two vectors.
Where θ is the angle between vectors. The Dot Product is written using a central dot. The angle is Orthogonal vectors.
V1V2 a1a2 b1b2 c1c2. The dot product is. The working rule for the product of two vectors the dot product and the cross product can be understood from the below sentences.
Dot product is an algebraic operation that takes two equal-length sequences of numbers usually coordinate vectors and returns a single number. Ab abcosθ. Remember that a Vector is a.
Geometrically it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them. Properties of Dot Product. Determine the angle between and.
The dot product of two vectors of magnitudes mathrmP 3 units and 5 units cannot be1 22 -2 3 20PW App Link - httpsbitlyYTAI_PWAP PW. The full version. Here are two vectors.
B a b cos θ. But thats not what is wanted here. This physics and precalculus video tutorial explains how to find the dot product of two vectors and how to find the angle between vectors.
We are given two vectors V1 a1i b1j c1k and V2 a2i b2j c2k where i j and k are the unit vectors along the x y and z directions. An exception is when you take the dot product of a complex vector with itself. A and b are the two vectors.
Calculate the dot product of A and B. The square root of the dot product of the vector by itself is equal to the length of. The dot product tells us how similar the directions of our two vectors are.
If two vectors are orthogonal then. A b This means the Dot Product of a and b. We can calculate the Dot Product of two vectors this way.
Again we need the magnitudes as well as the dot product. A is the magnitude length of vector a. The dot product of two vectors produces a resultant that is in the same plane as the two vectors.
In general the dot product of two complex vectors is also complex. C dot AB C 10000 - 50000i. The formula for the dot product in terms of vector components would make it easier to calculate the dot product between two given vectors.
The dot product of two vectors a and b is depicted as. So we need to multiply only non-zero values from both the vectors. A b a b cosθ Where.
Find the inner product of A with itself. They can be multiplied using the Dot Product also see Cross Product. θ is the angle between the two vectors a and b ranges between 0 to 180.
Ii jj kk 1. The result of a dot product is a scalar. The dot productthe scalar product is a gateway to multiply two vectors.
Geometrically the dot product is defined as the product of the length of the vectors with the cosine angle between them and is given by the formula. Y x y cos. The dot product is an operation that takes in two vectors and returns a number.
The dot product is also known as Scalar product. So the two vectors are. This formula gives a clear picture on the properties of the dot product.
The dot product can be either a positive or negative real value. The dot product between a unit vector and itself is 1. This is not efficient since a zero element multiplied with some other value from other vector will result zero.
The result is a complex scalar since A and B are complex.

How To Find The Scalar And Vector Product Of Two Vectors Easily How To Find Dot And Cross Product
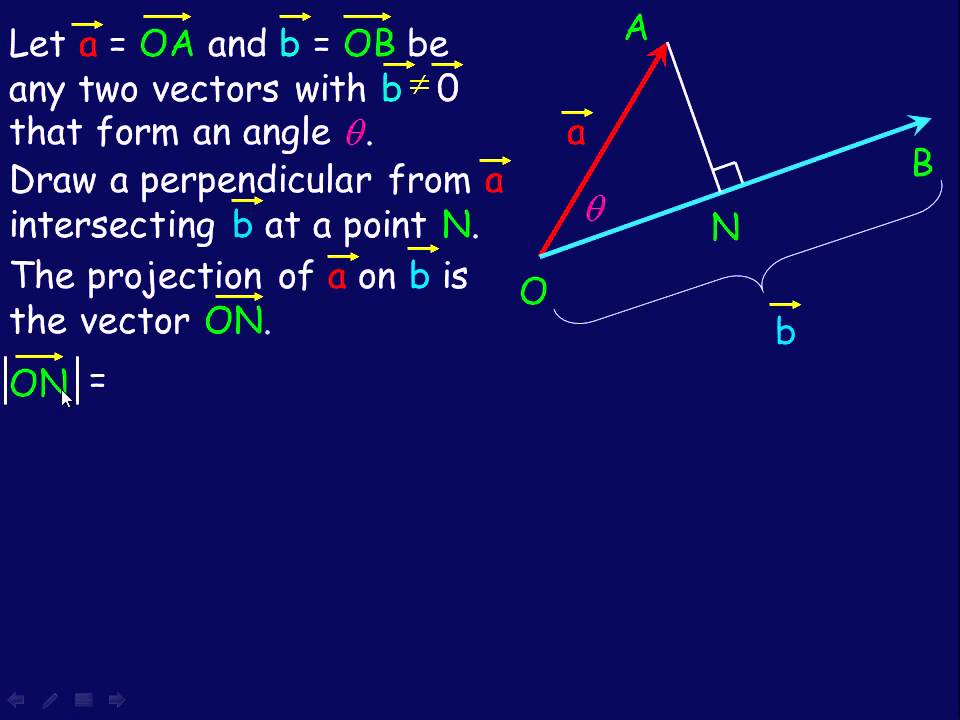
Applications Of The Dot Product Avi Calculus Mathematics 12th Maths

How To Memorize Things Commutative Vector

Product Of Vectors Vector Multiplication Vector Can

Dot Product A Plus Topper Reciprocalsystemofvectors Dots Positivity Commutative

Dot Product Explained Vector Calculus Calculus Mathematics Geometry

0 Response to "Dot Product of Two Vectors"
Post a Comment